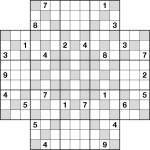
Samurai Star
Samurai Star XXXXX
Mar 12th
I haven’t posted a puzzle for a week (it’s been a busy week, mind!) so it’s time to make up for that, just in time for the weekend.
In this puzzle the aim is pretty simple: place 1 to 9 in each set of 9 squares starting and ending with a bold line, whether in a row or column, and similarly for each set of 9 squares starting and ending with a bold line in any of the shaded diagonals.
Good luck! ![]()
Samurai Star Inequality
Dec 8th
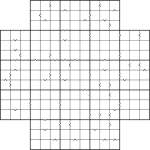
Samurai Star Inequality puzzle
I’m tempted to just say “good luck”, because frankly I think you’ll need it! Not of course in the literal sense, since this is an entirely logical problem, which requires absolutely no guess work, but in terms of finding the right areas to make progress quickly.
So having started at the end, let me introduce you to this Samurai Star Inequality puzzle. In all cases the “<” and “>” arrows point to the smaller number of each pair. Other than that it’s a regular Samurai Star – place 1 to 9 into each row, column and marked 3×3 box of each of the 5 underlying 9×9 grids (including the one in the centre).
And now back to the beginning: Good luck! ![]()
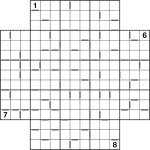
Two-away Samurai Star
Jul 16th
I made this puzzle yesterday but then went and forgot to post it (oops) so I’m making up for that now! It’s a Samurai Star with two-away markers, just as per the previous two puzzles I posted.
Place 1 to 9 into each of the rows, columns and 3×3 boxes of the 5 underlying Sudoku grids (including the one in the centre), whilst obeying the two-away grey bars. Squares with a grey bar between have a difference of 2 (e.g. 1&3 or 2&4), and those without a grey bar have a difference which is not 2.
There are only 4 givens to get you going, so good luck! ![]()
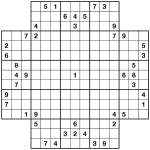
Wrap-around Consecutive Samurai Star
Jul 6th
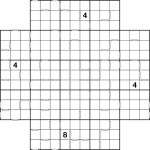
Wrap-around Consecutive Samurai Star puzzle
I seem to be posting more infrequently than I intend, so I thought I’d compensate with a puzzle that would take somewhat longer to complete! Here, then, is a wrap-around consecutive samurai star. All squares with consecutive values (a difference of 1) are marked with white bars, including those at opposite ends of rows and columns – wherever there isn’t a bar, the values are not consecutive.
The Sudoku logic takes a few twists here and there – in fact at one point near the end you will need to spot a particularly nasty hidden set in one region.
To solve the puzzle place 1 to 9 into each row, column and 3×3 box of each of the underlying 5 Sudoku grids (including the one in the centre). You’re only given 4 givens to get going, but with the consecutive information that’s all you need to find a unique solution.
Good luck! ![]()
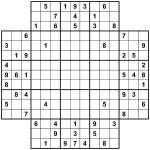
Samurai Star
May 23rd
You might be pleased to know that today’s puzzle is somewhat easier, despite being a lot bigger! It’s actually possible to comfortably solve this without making a single pencilmark, if you fancy an extra challenge. ![]()
It’s a Samurai Star / Flower Samurai puzzle. Just place 1 to 9 into each row, column and 3×3 box of the 5 underlying grids (there’s one in the centre too).
Good luck!
Samurai Star Killer Sudoku
Apr 29th
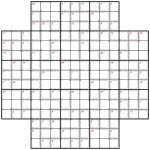
Samurai Star Killer (gentle) puzzle
“Star Killer” sounds like something out of science fiction, but it’s now definitely reality with this 5-grid Killer Sudoku puzzle. The actual Killer part uses the most basic logic imaginable, and there are a lot of ’singleton’ regions which I’ve never used in a Killer puzzle before. The reason for this is that I wanted to start at a gentle level – as a result this mostly solves like a regular Samurai Star (a.k.a. Flower Samurai) puzzle, with the Killer regions used occasionally to either get you going or help you out with a quick number along the way. It shouldn’t take you much over 20 or 30 minutes if you’ve solved this shape of Samurai before, and know what a Killer Sudoku is!
The rules are pretty simple: place 1 to 9 into each row, column and bold-lined 3×3 shape of each of the 5 underlying 9×9 grids (there’s one in the centre too), whilst also placing numbers so that the total in each dashed-line cage is equal to that given in the top-left corner. You may not repeat a number within a dashed-line cage.
The puzzle has rotation symmetry order 4, so the cages are in a pleasing pattern I hope – I particularly like the hole in the square in the centre! I think by and large that if you can create the cages or givens in a puzzle with the same order of symmetry that you have for the grid layout itself that this generally leads to a more pleasing appearance for the puzzle; but more than this, I find that this tends to follow through with the solving process, and you end up with pieces of the puzzle that feel ’sympathetic’ to one another, since the symmetry leads to related discoveries. However it’s perhaps not clear that this solving benefit carries through to a puzzle this large, and it’s probably the case that a puzzle with entirely random cages would feel just the same to actually solve at this size. But it wouldn’t look as nice!
Coming up in the following days I’m going to experiment in the space between Killer Sudoku and Ken Ken™ – in other words, using more operations than just addition, and possibly allowing repeated numbers in cages (although not on puzzles with 1-9 to place!). I already came across a puzzle called ‘Killer Sudoku Pro’ in the Saturday Telegraph newspaper (UK) – in this they keep the Killer Sudoku rules about not repeating digits in a cage, but specify different operations for cages (in actual fact the rules aren’t stated next to the puzzle in full, but I presume repeated digits are disallowed - it certainly solves okay with that assumption!). I haven’t seen anything precisely like that elsewhere and I thought it was actually quite fun (it wasn’t too hard!) so I’ll definitely try making some of those soon for sure. If you have any other ideas for how to mix these different types together feel free to post a comment!
Good luck!
Consecutive Samurai Star
Apr 17th
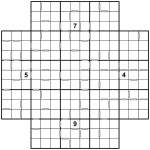
Samurai Star Consecutive puzzle
If the smaller consecutive puzzles weren’t enough of a challenge then this one should be! There are five overlaid 9×9 grids (including a ‘hidden’ one in the middle) which each need to have 1 to 9 placed into every row, column and bold-lined 3×3 box. On top of this you must obey the consecutive constraints – numbers with a white bar between are consecutive (12, 23, 34, 45, 56, 67, 78 or 89) and those without a bar between are not consecutive.
As you can see, the combination of tightly-overlaid grids and the consecutive marks means that very few givens are needed! Remember that none of these puzzles need ‘complex’ solving logic (you don’t need hidden or naked sets, X-wings or any other even more exotic strategy).
Good luck!
PS If there are any particular Sudoku or Samurai variants you’d like to see, please let me know and I’ll see what I can do!
Samurai Star
Apr 9th
One of my favourite Samurai Sudoku arrangements is the Samurai Star, also sometimes known as Flower Samurai. There’s been one every month in Sudoku Pro magazine for years, and what’s great about them is that because of the tight overlap of the underlying 9×9 grids there is some ‘new’ logic you can apply – essentially if a number occurs in a 3-cell row or column within a 3×3 box then that same number must also occur in the 3-cells that start 9 to the right/left/above/below (depending on whether it’s a 3-square row or column). It might sound confusing but it’s much more obvious when you try it out on an actual puzzle, and it’s one of those things that makes you go “ah, that’s nice” as you solve a puzzle – which is a good indicator of a decent design!
This particular puzzle has ‘8-way’ symmetry, which simply means that the pattern of givens is the same when reflected in both diagonals, and when rotated any multiple of 90 degrees, and when reflected and rotated.
The rules are simple: place 1 to 9 into each of the rows, columns and 3×3 boxes of the five underlying 9×9 Sudoku grids – four of them are obvious, and then there’s one in the centre too. It’s this centre grid that leads to the property I talk about above! You won’t find a unique solution if you omit this additional grid.

Recent Comments