Numberlink
Wraparound Numberlink
Sep 25th
 I’m currently working on a forthcoming book (The Mammoth Book of Brain Workouts, published next year in the UK by Constable & Robinson, and in the US by Running Press), and have been experimenting with something I wrote about briefly a few years ago but hadn’t really tried since – variants on Numberlink.
I’m currently working on a forthcoming book (The Mammoth Book of Brain Workouts, published next year in the UK by Constable & Robinson, and in the US by Running Press), and have been experimenting with something I wrote about briefly a few years ago but hadn’t really tried since – variants on Numberlink.
Numberlink puzzles have proved popular recently in various guises, including Flow Free and other apps on mobile devices such as the iPhone. There are quite a few such apps available, but none of them force a unique solution on the user (and generally the puzzles do indeed have many different solutions), which when you’re playing against a computer that grades you isn’t necessarily a problem since you can at least be marked correct/wrong automatically.
For a logic puzzle solver, such vague puzzles are perhaps a bit disappointing because you will reach a point during solving where you can’t eliminate any options because they may all be valid, despite being contradictory.
I’ve made a printed book of 200 of these Flow Free puzzles – you can get it from Amazon.com (currently $5.36) or Amazon.co.uk (£3.95) – and they’re actually quite fun to solve despite the multiple solutions (not all the puzzles have multiple solutions, but some do). Unlike traditional Numberlink the puzzles include an explicit rule that every cell in the grid must be used, which eliminates a lot of potential solutions and means the puzzles usually require some thought.
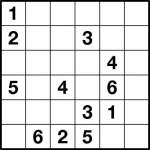
Toroidal numberlink 6×6 puzzle
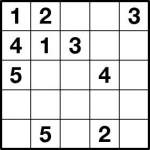
Toroidal numberlink 5×5 puzzle
But such multi-solution puzzles are not the kind of puzzle I usually post, so I’m going to stick to logic puzzles with unique solutions on this blog.
It turns out that if you allow lines on a Numberlink puzzle to wrap around one edge and come back on the other – so if a line goes off one end of a row or column it comes back on at the other end of the same row or column – that the puzzles get very difficult very quickly. In fact, even at 5×5 many such puzzles are very challenging. Once you get to 6×6, I have real trouble with them.
Here’s a 5×5 and a 6×6 puzzle for you to try. Let me know how you get on! There’s no explicit rule that every cell must be used – but as a hint I can tell you that they are anyway. There’s a unique solution to each puzzle.
More Diagonal Numberlink
Aug 5th
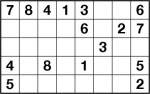
Diagonal Number Link 8×5 puzzle 2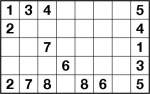
Diagonal Number Link 8×5 puzzle 1
Here’s two more, slightly larger, diagonal number link puzzles – these are 8×5. The problem with diagonal number link is that it’s very hard to constrain the puzzles to a unique solution without making them really quite easy, since lines essentially can’t run parallel for more than a couple of squares, otherwise they could swap over and back and produce at least two different solutions.
So in fact once you get over the slight confusion of diagonal lines, diagonal number link actually turns out to be easier I think, and these two puzzles do demonstrate the relatively easy nature – they can both be solved logically without too much effort. However I found them quite fun, none the less!
The finished puzzles look good though – all those diagonal lines make it seem as if you’ve just solved something really tricky… ![]()
Please see previous posts for the rules of number link and diagonal number link.
Diagonal Number Link!
Aug 4th
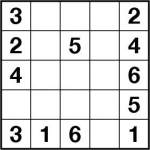
Diagonal Number Link 5×5 puzzle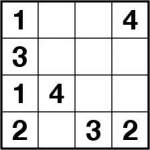
Diagonal Number Link 4×4 puzzle
If you thought toroidal number link was tricky, then how about diagonal number link?! In this variant the rules are exactly the same but now you can use diagonal lines as well as horizontal and vertical lines! The diagonal lines can only travel between diagonally-adjacent (diagonally touching) squares, and diagonal lines are allowed to cross. This is because the Number link rule is that “each square can only have a single line in it” – in the case of diagonal numberlink this does actually allow the lines to cross at the corner of certain squares. So just draw one line per pair of identical numbers, linking them together. In the unique solution all squares are used.
The first 4×4 puzzle is very easy but despite being very easy it’s still a bit confusing to actually solve, so I’d suggest trying it first.
The 5×5 puzzle isn’t exactly difficult either, but it might at least give you a minute or so of amusement! I found it quite interesting to solve at least.
Toroidal Number Link
Jul 31st
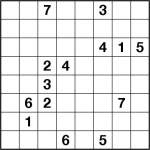
Toroidal Number link 8×8 puzzle
Number Link at sizes up to around 10×10 may not necessarily be hugely challenging for everyone, but I bet you now that this puzzle certainly will be! Despite being only 8×8 it is really very difficult indeed. Or perhaps that’s just me – I’d love to hear that someone finds it easy, but I’m not expecting anyone to!
The rules of this puzzle are, however, very simple:
- Connect each pair of identical numbers with a single line
- Lines can travel horizontally or vertically between squares
- Only one line can enter any square (this means lines cannot cross or overlap in any way)
- Your lines may wrap around from one side of the puzzle to the other, so for example if you travel off the right-hand end of a row then your line will continue on in the left-most square of that row
There is a unique solution to this puzzle, and it uses every square. However, the solution is unique even without the constraint that it uses every square.
If you’ve played toroidal sudoku then you’ll hopefully understand how the wrap around works – when you go off the top of a column you come back on the bottom, and similarly (as stated above) for rows. If the basic rules of Number link itself confuse you, take a look back at a post a few days ago for an example.
And good luck – I think you’ll need it! ![]()
Number Link, Link, Link, Link
Jul 31st
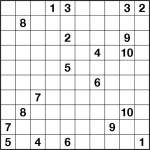
Numberlink 10×10 puzzle 2 (fixed)
Numberlink 10×10 puzzle 1
When I first tried a Number link puzzle a few years back I didn’t like it at all – it wasn’t immediately clear how to go about solving it, and I didn’t see how I’d ever find it fun. However jump forward to now and I find them really enjoyable, perhaps because it usually is hard to know how to solve them and so you need some fresh thinking each time you try one.
It’s not the only puzzle I’ve had this experience with. There’s a box-shading puzzle called Heyawake that I found horribly mechanical and tedious when I first tried one, probably because at that point I could only tackle the easy ones and so mainly I got stuck when I failed to spot where I could directly apply a solving rule. However a couple of years ago I tried it again and it soon turned into one of my absolute favourites, although it hasn’t quite pushed Nurikabe off its crown of being my personal number one.

Numberlink 10×10 puzzle 4
Numberlink 10×10 puzzle 3
It works in reverse too, however. I used to really enjoy Filomino puzzles, but now I mostly find them rather dull – I think that once you get good at certain puzzles you hit a natural wall in difficulty where making them any trickier without requiring what is essentially just guesswork is a real challenge, so you find most puzzles mostly easy. In a great puzzle (like Sudoku), you’ll always find some puzzles tricky no matter how knowledgeable you get, but not all puzzle types behave so gracefully.
The point of all this is that Number link is one of those puzzles that – for me at least – always presents a challenge, and makes me think anew each time I try one. And because it can be infuriatingly tricky it’s also capable of giving me a great deal of satisfaction when I do solve a puzzle.
The Number link examples I’ve posted so far have been pretty easy, so I thought I’d post a few more that were a bit harder. All of these have at least a couple of obvious moves, so it’s certainly possible to make trickier 10×10 puzzles than these, but they do present at least a bit more of a challenge. I’ve arranged them by what I considered increasing order of difficulty, but you may disagree, depending upon how inspired you are as you tackle each puzzle!
The rules are simple: connect each number to its identical partner using only horizontal and vertical lines. Only one line may pass through a square, so lines cannot cross or overlap. There is only one solution. In all of these puzzles the unique solution also uses every square. Both of these last two facts are very useful in narrowing down possible solutions! Take a look at my previous posting for an example solution.
Good luck! ![]()
Edit: The first version of this post included a puzzle (number 2) that had lots of different solutions that didn’t use all squares – I’ve now replaced it with an alternative puzzle. See comments.
Number Link 10×10
Jul 27th
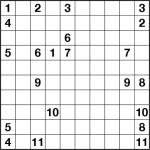
Numberlink 10×10 puzzle 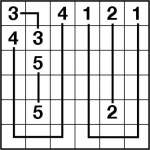
Numberlink example solution
I’ve had a couple of emails and comments suggesting that it would have been easier if I’d included an example with yesterday’s Number Link puzzle, so I’ve made up for that today with both another puzzle (10×10 this time, and not too taxing I hope) and a small 6×6 example of what a finished puzzle would look like: each pair of numbers is linked by a line which travels horizontally or vertically through the squares, and no square is visited more than once (and therefore no lines cross or overlap at any point).
Good luck! ![]()
Number Link
Jul 26th
Over the past few years I’ve made at least one example of pretty much every reasonably popular Japanese number puzzle, but with one notable exception: Number Link. In this puzzle the aim is to draw lines connecting squares with identical values in, but without these lines crossing over or visiting any square more than once. The lines can also only travel horizontally or vertically, not diagonally.
In a completed Number Link puzzle, the lines will be placed such that every square is used – and that solution is guaranteed to be the unique solution too. The rules are not, however, always stated that strongly. In fact the most common form of the rules simply states that you must connect all sets of numbers, with an implied assumption that there is a unique solution, and furthermore again only an implication that that solution uses every square. But in terms of solving the puzzles in practice, it’s fair to assume that:
- There is a unique solution, and that unique solution happens to use every square
This assumption means that whilst solving a puzzle you can make various deductions about how lines can and cannot go based on noting what would make a puzzle non-unique, or not use every square. Once you discard these assumptions (as you need to do when creating the puzzle, since you can’t assume uniqueness without proving it!) it’s typically much harder.
It stands to reason that as puzzles get larger that they can get much trickier, but that isn’t always the case: today’s first example puzzle, whilst quite large at 20×9, is actually really easy, as you’ll probably find out when you try solving it! ![]()


Recent Comments