Posts tagged Division
Samurai Toroidal Killer Sudoku Pro 13-grid
May 7th

Samurai Toroidal 13-grid Killer Sudoku Pro puzzle
Now this is a puzzle I can state with confidence that you won’t have seen before. It’s a Killer Sudoku Pro puzzle – i.e. a Killer Sudoku with -, x and / regions too; but more than that it’s a Samurai Killer Sudoku Pro made out of 13 grids; and then further still the cages are toroidal, both around the edge of the grid and across the gaps. In other words, the Killer Sudoku Pro regions aren’t bounded by the actual physical layout of the 13-grids – they either jump the gap (in a straight line) or wrap around the edges of the puzzle (again in a straight line, albeit one that jumps to the other side!).
If you like huge puzzles then you should really enjoy this, assuming you can print it out large enough to actually have a chance of solving it! For everyone else, I’ll post some more smaller puzzles soon! It’s not actually very difficult, logically, but completing the whole thing would still take a fair while – perhaps a couple of hours, I think.
The rules are:
- Place 1-9 into each row, column and 3×3 bold-lined box of each of the 13 underlying 9×9 Sudoku grids
- Place numbers into each dashed-line cage so that all together they give the total at the top-left of the cage once the given operation is applied – for subtraction and division start with the largest number in the cage and then subtract/divide-by the other numbers.
- Numbers can not be repeated in a cage.
- Some cages continue across the gaps – just use an imaginary straight-line rule to follow them on and find the rest of the cage (so for example if a cage runs across a gap in the 3rd row down, it continues on the other side of the gap also on the 3rd row down)
- Some cages continue across the edges of the grid – these wrap around to the same row or column on the opposite side of the puzzle
If you try it: Good Luck!
As Easy as 11, 22, 33… a Killer CalcuDoku
May 3rd

As easy as 11, 22, 33 Killer CalcuDoku
Here’s a relaxing puzzle for a Sunday… or maybe not! Can you complete this Killer CalcuDoku puzzle made up of 1s, 2s and 3s?
Place 11, 12, 13, 21, 22, 23, 31, 32 or 33 into each square so that the result of applying the specified operation to each cage is the given number. (Start with the highest number in the cage for subtraction and division cages). Also, can you obey the standard Sudoku constraints: place each of the 9 different numbers once per row, column and bold-lined 3×3 box? You can repeat numbers within a cage, however, if you wish (which is why it’s a Killer CalcuDoku, not a Killer Sudoku Pro, in my terminology! It’s also why it has solid cages, rather than dashed-line cages).
The logic isn’t too tricky, but for speed you might find a calculator helps you make a few of the logically easy deductions… ![]()
Good luck!
Killer CalcuDoku +/-
May 2nd

Killer CalcuDoku +/- 6×6 puzzle
There’s a lot of very interesting puzzle space to explore between the extremes of Killer Sudoku and KenKen (a trademark of Nextoy LLC, so I will always refer to this as CalcuDoku from now on, unless anyone suggests a better name!).
I’m going to define two in-between puzzles, giving a continuum like this:
- Killer Sudoku
- Killer Sudoku Pro – Killer Sudoku with extra operations (+, -, x, /)
- Killer CalcuDoku – Killer Sudoku Pro with repeated digits in cages, like CalcuDoku
- CalcuDoku – Killer CalcuDoku puzzles without box constraints (e.g. no 3×3 boxes)
To avoid confusion I’m going to draw Killer Sudoku and CalcuDoku the way they always are – with dashed-line cages in the first case and bold lines between squares for the latter (replacing the traditional Sudoku bold lines). Then to distinguish the others, Killer Sudoku Pro will appear exactly like Killer Sudoku except that there will be additional operators within the grid (for operator-less ones I’ll include a question mark “?” or similar after each clue). Killer CalcuDoku, meanwhile, will appear exactly like today’s puzzle – with solid cages within the main puzzle.
Now just to spice things up further, I’m going to mess around with how the puzzles work. Remember that the key difference between Sudoku and Killer Sudoku is that the digits now actually have value as well – so by fiddling with those values we can create an infinite range of new puzzles that solve in quite different ways.
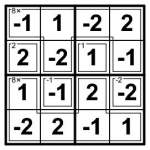
Example Killer CalcuDoku +/- solution
Today is a good example: here’s a 6×6 +/- Killer CalcuDoku. The aim is to place -3, -2, -1, 1, 2 and 3 into each row, column and 2×3 bold-lined box, and to place numbers so that the inner cages compute to the value given when applying the stated operation to the set of numbers in that cage. Subtraction and division are again defined as starting with the highest number in that cage (so remember that 2>-3!) and then applying all the other numbers in any order – so for example the solution to a “4-” cage could be “1 and -3″. Confused? See, I said it would mix things up! (1 – -3 = 4)
I’ve included an example (trivial) 4×4 Killer CalcuDoku +/- solution so you can be sure you understand how it works. But you might not need it – it’s actually a very gentle puzzle I’ve attached, as you’ll probably soon find out… (well, once you get your head around the negative numbers!)
Good luck!
Killer Sudoku Pro / All Signs
May 1st

Killer Sudoku All Signs puzzle
Here’s a Killer Sudoku with “all the signs”, or Killer Sudoku Pro if you prefer. If you’ve got any ideas for a better name let me know! ![]()
As in a regular Killer puzzle, you can’t repeat a digit within the solution to any cage. Unlike in a regular Killer, all non-single cages specify the operation that is applied to produce the result given. If the operation is + or x then just add or multiply all the digits to give that total. For subtraction and division you must start with the largest number in the region and subtract or divide the other numbers from that to give the stated result (this is what you’d do intuitively, I think, but since these operations aren’t commutative it’s necessary to state this!) Other than that, regular Sudoku rules apply: place 1 to 9 into each row, column and bold-lined 3×3 box.
The logic is once again simple, as a first example of this puzzle type, but I think the wider range of operations brings a freshness to the puzzle. Let me know if you agree (or disagree!).
Good luck!

Recent Comments