Samurai Variants
Samurai 8X
Sep 6th
When I was making Sudoku Xtra 10 I wanted to put in a really big Samurai Sudoku puzzle. In the end because I had a square page area available beneath the instructions I went with a 13-grid one (just as a one-off to see what sort of reaction it got!) but I had started off intending to use an 8-grid one. It seemed a shame to let it go to waste, so I’m posting it here.
- Place 1 to 9 into each row, column, main diagonal and 3×3 box of each of the eight 9×9 grids.
- Note that, as in a regular Sudoku, only the rows, columns and main diagonals within the eight underlying 9×9 grids are guaranteed to contain all of 1-9. Any row, column or diagonal not entirely within a single 9×9 grid has no restriction on its content.
So best of luck – you don’t need it, but it might help anyway! ![]()
Samurai Killer Sudoku Pro 6×6
Apr 27th

Killer Sudoku Pro 6×6 Samurai puzzle
It’s been quiet here recently – much of my effort has been going on my UK General Election site, How To Vote, although Sudoku Xtra 6 was out on Saturday too. Anyway, there are still 10 days to go to the election but after that I’ll get some time back!
However I thought I should finally post another puzzle – so here one is. Place 1 to 6 in each row, column and 2×3 box (rows and columns are defined by the three underlying 6×6 grids, which you have to infer from the stepping). Also place numbers so that the value at the top-left of each dashed-line cage results from applying the operation between all the value in that cage. For subtraction and division start with the largest value.
Have fun! ![]()
Samurai Star XXXXX
Mar 12th
I haven’t posted a puzzle for a week (it’s been a busy week, mind!) so it’s time to make up for that, just in time for the weekend.
In this puzzle the aim is pretty simple: place 1 to 9 in each set of 9 squares starting and ending with a bold line, whether in a row or column, and similarly for each set of 9 squares starting and ending with a bold line in any of the shaded diagonals.
Good luck! ![]()
Samurai Odd-Pair Sudoku
Mar 1st
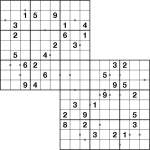
Samurai-2 Odd Pair Sudoku puzzle
One of the brand new puzzles in Sudoku Xtra issue 4 is Odd-Pair Sudoku, which I wrote about last week here on my puzzle blog. As well as some regular 9×9 puzzles I also included a large 5-grid Odd-Pair Samurai puzzle, and to illustrate how the puzzle worked I included a small solved example alongside. A full 5-grid Samurai was too big to fit sensibly in the example box, so I made a 2-grid Samurai version just for that little solution area. So that’s the solution used, but what about the puzzle itself? Well, here it is! (And so if you want to check your solution – yes, it’s printed in Sudoku Xtra issue 4! Page 19, to be precise).
The rules, in case you missed them, are really simple:
- Place 1 to 9 in each row, column and bold-lined 3×3 box of the two 9×9 Sudoku grids
- Every pair of squares with an ‘o’ circle between them must sum to an odd value. (’o’ for odd). So for example you could have “3 o 6″, but not “3 o 5″ (since that would sum to 8, an even number).
This variant is fun because it eliminates lots of possibilities from squares relatively quickly, so you’re left with more deductive logic and less pencil-mark housekeeping.
Good luck! ![]()
Crazy Calcudoku!
Feb 23rd
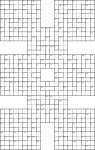
Samurai 8-grid Calcudoku puzzle
Here’s probably the largest Calcudoku puzzle you’ve ever seen! It’s made up of 8 underlying 9×9 grids, each of which must have 1 to 9 placed into each row and column, and then on top of this I’ve added the familiar Calcudoku regions.
For each Calcudoku region just place numbers such that the total after applying the stated operation between the numbers in the region is the one given. For example, 7+ could be solved by 3 and 4 (3+4). For subtraction and division start with the largest number in the region, so 1- could also be solved with 3 and 4 (4-3).
Just to make it really clear, there are no 3×3 Sudoku box regions in this puzzle – just the 8 sets of rows and columns.
Good luck! ![]()
Samurai Killer Calcudoku
Jan 28th

Samurai Killer Calcudoku puzzle
I haven’t posted much here recently because I’ve been spending my time on Sudoku Xtra, so here’s a large puzzle to fill the void a bit.
This is a five-grid Samurai Killer Calcudoku:
- Place 1 to 9 into each row, column and 3×3 box of the five underlying 9×9 Sudoku grids
- Place numbers into the Calcudoku dashed-line cages to fulfil the results at the top-left of each cage. The given operator when applied between all of the numbers must give the stated result, e.g. the solution to “5+” could be “2+1+2″. For subtraction and division start with the largest number, so for example “3-” could be “6-3″.
- Numbers can be repeated in Calcudoku cages, subject to the row, column and 3×3 box constraints.
Unlike my other puzzles I haven’t used any symmetry in this one, but I’m not sure it’s really that obvious on a puzzle like this one. It’s not especially hard, but with so many places to potentially go it might take you a little while.
Good luck! ![]()
Samurai Star Inequality
Dec 8th
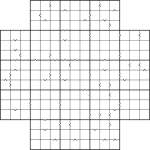
Samurai Star Inequality puzzle
I’m tempted to just say “good luck”, because frankly I think you’ll need it! Not of course in the literal sense, since this is an entirely logical problem, which requires absolutely no guess work, but in terms of finding the right areas to make progress quickly.
So having started at the end, let me introduce you to this Samurai Star Inequality puzzle. In all cases the “<” and “>” arrows point to the smaller number of each pair. Other than that it’s a regular Samurai Star – place 1 to 9 into each row, column and marked 3×3 box of each of the 5 underlying 9×9 grids (including the one in the centre).
And now back to the beginning: Good luck! ![]()
Inequality Sudoku
Dec 4th
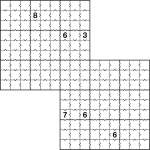
Inequality 2-grid Samurai Sudoku
Inequality jigsaw 6×6 Sudoku puzzle
On the Sudoku Xtra forums Marilyn suggested the great idea of an inequality Samurai puzzle for issue 2, so I’ve been having a look at doing this. And here’s the first result!
I’ve started off with a regular 6×6 jigsaw Sudoku, but have added inequalities, just to get you warmed up, then I’ve included my first ever Samurai Inequality Sudoku puzzle, albeit a 2-grid one for now.
You’ll notice in both puzzles here that I have included all inequality arrows, so you have far more information than you need – this is deliberate, to make them easier! On the 6×6 puzzle there are five really nice diamond shapes in the centre area, but in general I think having all the arrows is ugly (or lazy!) so I don’t plan to include them again in future (just as I’ve never included them in past published inequality/Futoshiki puzzles).
The rules of Inequality Sudoku are pretty simple – just place the numbers as you would in a regular Sudoku (or regular Jigsaw Sudoku in the 6×6 case), but obey the less-than (”<”) and greater-than (”>”) signs between squares. These indicate that the value of the number in a square is either less than or greater than its neighbour. And that’s it! ![]()
Good luck!
Two-away Samurai Jigsaw
Jul 17th
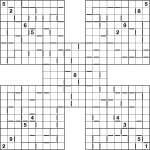
Two-away Samurai Jigsaw puzzle
Here’s a puzzle for the weekend – it’s a 5-grid samurai sudoku where in the corner grids a couple of the 3×3 regions have had their outlines tweaked to turn them into jigsaw sudoku puzzles, with full 8-way symmetry. There are very few givens, which means you’ll need to take full advantage of the two-away markers that are also in the grid. The grey rectangles indicate all neighbouring squares where the difference is 2 (e.g. 1&3 or 6&8) – even without precise values they can also be useful for quickly indicating where a chain of squares are all odd or all even.
Good luck! ![]()
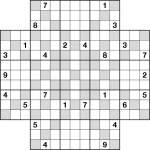
Two-away Samurai Star
Jul 16th
I made this puzzle yesterday but then went and forgot to post it (oops) so I’m making up for that now! It’s a Samurai Star with two-away markers, just as per the previous two puzzles I posted.
Place 1 to 9 into each of the rows, columns and 3×3 boxes of the 5 underlying Sudoku grids (including the one in the centre), whilst obeying the two-away grey bars. Squares with a grey bar between have a difference of 2 (e.g. 1&3 or 2&4), and those without a grey bar have a difference which is not 2.
There are only 4 givens to get you going, so good luck! ![]()


Recent Comments