Consecutive Sudoku
Diagonal Non-Consecutive Sudoku
Jun 19th
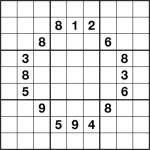
Sudoku Non-consecutive-diagonal 9×9 1 puzzleThis is a non-consecutive-diagonal sudoku puzzle. No digit may be diagonally-adjacent to a consecutive digit. But as you can see from the givens, consecutive numbers can be adjacent horizontally or vertically. What you can’t have, for example, is a 1 diagonally next to a 2 because the 1 & 2 are ‘consecutive’ (have a numeric difference of 1).
Consecutive Snake Sudoku
Jun 15th
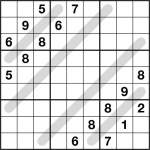
Sudoku Snake 9×9 1 puzzleHere’s something a little different – a consecutive snake sudoku.
Each of the shaded snakes consists of only ‘consecutive’ cells along its length, which means that any two cells joined by a snake must have values with a difference of 1, such as 2&3 or 7&8. So for example the 4-square-long snake at the top-left might have 2323 along its length, or any valid fit such as that.
In addition follow usual sudoku rules. Also note that only the cells joined by the snakes have any special relationship – any other pair of cells may or may not be consecutive (unlike in regular consecutive sudoku).
Non-Consecutive Sudoku
Mar 28th
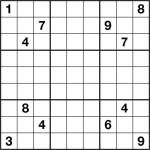
Non-consecutive Sudoku puzzleI’m currently working on a new book of sudoku variants for a major publisher, so have been making lots of new puzzles of different types. From time to time I’ll probably post again here with some examples of these.
I thought I’d start off with Non-Consecutive Sudoku. This is a minor variant on Consecutive Sudoku, where all the rules of standard Sudoku apply but there is one additional constraint:
- Neighbouring squares are not consecutive. This means there is never a difference of ‘1′ between two edge-adjacent squares (i.e. touching, not including diagonally).
For example, if a square contains ‘3′ then any neighbouring square cannot contain either ‘2′ or ‘4′.
Good luck!
Consecutive Skyscraper
Nov 24th
It’s been a while since I posted a new puzzle here, what with all the excitement about Sudoku Xtra magazine, so I thought I had better do something about that right now! So to that end, here’s something a little bit unusual – a Consecutive Skyscraper puzzle.
Now Consecutive Skyscraper may sound like a brief description of downtown Manhattan, but in fact it’s a puzzle with pretty simple rules:
- Place 1 to 8 in each row and column
- Obey the Skyscraper constraints: each number outside the grid reveals the number of ‘visible’ digits looking along that row/column, where higher digits obscure all lower ones
- White bars between squares reveal all consecutive squares – those where the difference is one (such as 1&2, 2&3, etc). Squares without white bars between are not consecutive
If that isn’t detailed enough for you, try clicking the relevant links on the right, or here’s what I wrote back in April about Skyscraper puzzles:
In a Skyscraper puzzle you place numbers in a grid whilst obeying ‘building height’ constraints around the edge. These building height constraints specify the number of notional buildings you could see whilst standing at the edge of the puzzle and looking in, whereby a taller building completely hides the view of any shorter building. The idea is that a digit ‘1′ in the grid is a building 1 storey high; a digit ‘2′ in the grid is a building 2 storeys high, and so on.
If you had a very simple 3×3 Skyscraper puzzle, here’s the potential solutions to each of the possible clues:
- 1: can be either 3 2 1 or 3 1 2, with the ‘3′ hiding both the other digits
- 2: can be 1 3 2 or 2 3 1 or 2 1 3.
- 3: can only be 1 2 3 because this is the only way to see all of the buildings.
Good luck! ![]()
Wrap-around Consecutive Samurai Star
Jul 6th
Wrap-around Consecutive Samurai Star puzzle
I seem to be posting more infrequently than I intend, so I thought I’d compensate with a puzzle that would take somewhat longer to complete! Here, then, is a wrap-around consecutive samurai star. All squares with consecutive values (a difference of 1) are marked with white bars, including those at opposite ends of rows and columns – wherever there isn’t a bar, the values are not consecutive.
The Sudoku logic takes a few twists here and there – in fact at one point near the end you will need to spot a particularly nasty hidden set in one region.
To solve the puzzle place 1 to 9 into each row, column and 3×3 box of each of the underlying 5 Sudoku grids (including the one in the centre). You’re only given 4 givens to get going, but with the consecutive information that’s all you need to find a unique solution.
Good luck! ![]()
(Non-consecutive) Consecutive Sudoku 12×12
Jun 30th

Consecutive 12×12 Sudoku puzzle
After a bit of a break to meet a major book deadline – the non-consecutive part of the title of this posting – I’m back with what seems to be one of the most popular types of puzzle, a Consecutive Sudoku. I wanted something a little bit different, though, so this is a Consecutive Sudoku 12×12. I personally always find Sudoku 12×12 pretty similar to regular 9×9 Sudoku to solve, unlike something like 16×16 which personally I’d never really bother with (apologies to anyone who loves them!).
In order to make the consecutive nature of the 12 possible values obvious, I’ve used one- and two-digit numbers rather than digits and letters. So the rules are simple: place 1 to 12 into each row, column and 4×3 box whilst obeying the white consecutive markers. Wherever there is a white consecutive marker between two squares then the difference of value in those two squares is 1; and conversely whereever there is no marker the difference is always greater than 1.
So sorry for the break – hopefully ‘normal’ service will now be resumed! ![]()
And good luck with the puzzle!
Consecutive Skyscraper 8×8
Jun 17th
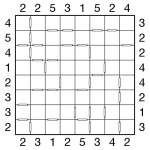
Consecutive Skyscraper 8×8 puzzle
Here’s a combination I haven’t posted before – a standard skyscraper puzzle with the addition of consecutive markers between adjacent squares. This allows the creation of an 8×8 puzzle without needing to also add Sudoku boxes.
The rules are as follows:
- Place 1-8 in each row and column
- Numbers outside the grid reveal the number of ‘visible’ numbers looking along that row/column, where higher numbers obscure lower ones
- White bars between squares reveal all consecutive squares – those where the difference is one
Good luck! ![]()
Wrap-around Consecutive 3-grid 6×6 Samurai Skyscraper
May 18th
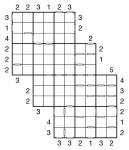
Wrap-around Consecutive 3-grid 6×6 Samurai Skyscraper puzzle
Another mouthful of a puzzle name, but in essence simply a development of the previous puzzle I posted. This time we still have the wrap-around consecutive-ness, but I’ve extended it to a samurai puzzle and added in skyscraper clues. To keep it reasonable, I’ve reduced the underylying Sudoku size to 6×6, however!
What’s particularly fun about the wrap-around markers is that they warp from one side of the puzzle to the same row/column on the opposite side – for the centre two columns this means that they constrain the values of two numbers 10 squares apart.
So the full rules are:
- Place 1 to 6 into each row, column and 2×3 bold-lined box of each of the three underlying 6×6 grids
- White bars show that adjacent cells are consecutive – i.e. 1&2, 2&3, 3&4, 4&5 or 5&6; those squares without a white bar between are non-consecutive
- White bars are shown where appropriate even on the edges of the grid – they indicate how the cell relates to the square at the far end of this row/column of numbers. Remember that the lack of such a white bar means that these wrap-around squares are non-consecutive.
- Skyscraper clues reveal how many numbers can be ’seen’ from that clue number counting in along the adjacent row/column, where higher numbers obscure all lower numbers (see previous puzzles for more detailed instructions)
Just to clarify, if adjacent numbers are equal (which is possible if they’re at far sides of the grid from one another) then these count as non-consecutive.
Good luck! ![]()
Consecutive Wrap-Around Sudoku
May 16th
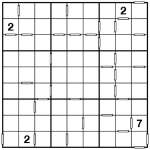
Consecutive Wrap-around Fiendish Sudoku puzzle
Here’s a slight twist on Consecutive Sudoku – I’ve included ‘wrap-around’ consecutive indication, where rows that start and end in consecutive digits have a white bar at the start and end of the row to show this, and similarly for columns. If they’re non-consecutive then there is no white bar. Similarly between all other squares: a white bar indiciates that two squares are consecutive, and no white bar means that they are non-consecutive.
‘Consecutive’ means that the difference between the numbers is ‘1′, i.e. they are 1&2, 2&3, 3&4, 4&5, 5&6, 6&7, 7&8 or 8&9. Other than this it’s a regular Sudoku – place 1 to 9 into each row, column and bold-lined 3×3 box.
This is also a difficult Sudoku, so if you can solve it under 20 minutes that would definitely be good going. Don’t forget about the non-consecutiveness – this is very important to reach the solution, and don’t forget about the wrap-around!
Good luck!
Consecutive 5-grid Samurai Sudoku
Apr 24th
I thought it would be a nice idea to create a large Consecutive Sudoku for the weekend! And so here one is: a 5-grid Samurai Consecutive Sudoku. As you can see, there are very few givens to start with, so it will hopefully be at least a bit of a challenge! (It shouldn’t be as tricky as the Skyscraper version, at least once you get going!).
I’ve also decided to make Consecutive Sudoku the ‘puzzle of the month’ (”Masterclass”) puzzle in Sudoku Pro issue 45, which should be out in just under 2 months I think. Hopefully I’ll also make a book of them available online soon(ish!).
The rules for this Consecutive Samurai are simple: place 1 to 9 into each row, column and bold-lined 3×3 box of each of the 5 Sudoku grids, whilst also obeying the consecutive constraints – numbers with a white bar between are consecutive, whilst those without a white bar between are not consecutive. ”Consecutive” means that the difference between the values in the two squares is exactly 1: i.e. 1&2, 2&3, 3&4, 4&5, 5&6, 6&7, 7&8 or 8&9.
Good luck!


Recent Comments