Odd Pairs
Samurai Odd-Pair Sudoku
Mar 1st
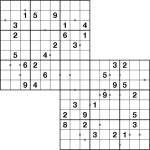
Samurai-2 Odd Pair Sudoku puzzle
One of the brand new puzzles in Sudoku Xtra issue 4 is Odd-Pair Sudoku, which I wrote about last week here on my puzzle blog. As well as some regular 9×9 puzzles I also included a large 5-grid Odd-Pair Samurai puzzle, and to illustrate how the puzzle worked I included a small solved example alongside. A full 5-grid Samurai was too big to fit sensibly in the example box, so I made a 2-grid Samurai version just for that little solution area. So that’s the solution used, but what about the puzzle itself? Well, here it is! (And so if you want to check your solution – yes, it’s printed in Sudoku Xtra issue 4! Page 19, to be precise).
The rules, in case you missed them, are really simple:
- Place 1 to 9 in each row, column and bold-lined 3×3 box of the two 9×9 Sudoku grids
- Every pair of squares with an ‘o’ circle between them must sum to an odd value. (’o’ for odd). So for example you could have “3 o 6″, but not “3 o 5″ (since that would sum to 8, an even number).
This variant is fun because it eliminates lots of possibilities from squares relatively quickly, so you’re left with more deductive logic and less pencil-mark housekeeping.
Good luck! ![]()
Sudoku Odd Pairs – a new variant!
Feb 23rd
Now here’s something I can guarantee you won’t have seen before, because I just invented it! ![]() Well, I suppose with a world of people creating Sudoku variants it’s possible there’s been something similar before, but I’ve bought a lot of puzzle magazines and books and never come across it, so perhaps I should say I can just about guarantee you won’t have seen it before!
Well, I suppose with a world of people creating Sudoku variants it’s possible there’s been something similar before, but I’ve bought a lot of puzzle magazines and books and never come across it, so perhaps I should say I can just about guarantee you won’t have seen it before!
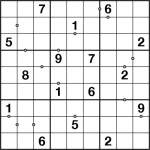
So the puzzle is Sudoku Odd Pairs, and as the name implies it’s all about odd pairs of numbers. Now you may have come across regular odd/even Sudoku before, and to be honest it’s a pretty dull variant (which is why I’ve never made them) – in fact if you for example shade all squares that contain even numbers it just breaks into two separate puzzles that overlap, and if you instead mark just a selection of even (or odd) squares then it’s only interesting until you work out whether the shaded squares are odd or even.
Sudoku Odd Pairs isn’t like that, because instead of marking squares what I’ve done is mark pairs of squares. Some squares have a grey circle between them – you can think of this as an O for Odd. What this means is that the sum of the solution of these two squares is odd. I don’t mark all odd pairs, however, because if you do this you need only one single digit in the entire grid (any of the givens will do) to work out which squares are odd and which even and then you end up with the above boring variant again. So this is important: you can’t infer anything about squares without an O between them – only those with the O between.
It turns out (at least in my opinion!) that this is actually a really fun variant, because you end up with many interesting parts of each puzzle where you realise you can force sets of odds or evens into groups of squares (and not just those with the Os on), which in turn effect the rest of the puzzle. You do to an extent need to make pencil marks when solving, as in Consecutive and many other variants, but the nature of the constraint is such that the number of pencil marks is roughly halved relative to most other variants which (for me at least) makes it far more fun.
I’ve talked about it enough. Try out the puzzle here and let me know what you think!
And if you would like more of these, I’m putting them into Sudoku Xtra issue 4 (out soon!), including a nice Samurai version.

Recent Comments