Flow Free book coverI’m currently working on a forthcoming book (The Mammoth Book of Brain Workouts, published next year in the UK by Constable & Robinson, and in the US by Running Press), and have been experimenting with something I wrote about briefly a few years ago but hadn’t really tried since – variants on Numberlink.

Numberlink puzzles have proved popular recently in various guises, including Flow Free and other apps on mobile devices such as the iPhone. There are quite a few such apps available, but none of them force a unique solution on the user (and generally the puzzles do indeed have many different solutions), which when you’re playing against a computer that grades you isn’t necessarily a problem since you can at least be marked correct/wrong automatically.

For a logic puzzle solver, such vague puzzles are perhaps a bit disappointing because you will reach a point during solving where you can’t eliminate any options because they may all be valid, despite being contradictory.

I’ve made a printed book of 200 of these Flow Free puzzles – you can get it from Amazon.com (currently $5.36) or Amazon.co.uk (£3.95) – and they’re actually quite fun to solve despite the multiple solutions (not all the puzzles have multiple solutions, but some do). Unlike traditional Numberlink the puzzles include an explicit rule that every cell in the grid must be used, which eliminates a lot of potential solutions and means the puzzles usually require some thought.


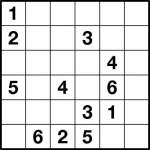
Toroidal numberlink 6×6 puzzle


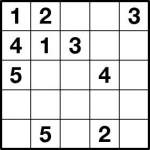
Toroidal numberlink 5×5 puzzle

But such multi-solution puzzles are not the kind of puzzle I usually post, so I’m going to stick to logic puzzles with unique solutions on this blog.

It turns out that if you allow lines on a Numberlink puzzle to wrap around one edge and come back on the other – so if a line goes off one end of a row or column it comes back on at the other end of the same row or column – that the puzzles get very difficult very quickly. In fact, even at 5×5 many such puzzles are very challenging. Once you get to 6×6, I have real trouble with them.

Here’s a 5×5 and a 6×6 puzzle for you to try. Let me know how you get on! There’s no explicit rule that every cell must be used – but as a hint I can tell you that they are anyway. There’s a unique solution to each puzzle.