Posts tagged Inequality
Futoshiki puzzles
Dec 19th
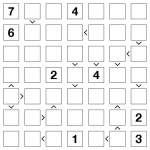
Futoshiki 7×7 puzzle
Futoshiki 6×6 puzzle
It’s been a little quiet here the past week or so due to circumstances beyond my control, but in preparation for the launch of Sudoku Xtra issue 2 tomorrow I thought it would be fun to post a couple of left-over puzzles here. These are nothing particularly unusual, I’m afraid – just some regular Futoshiki puzzles, in fact, but I don’t think I’ve posted any of these to this blog before so it was probably about time I did!
The rules of the puzzle are really simple – just place 1 to 6 or 1 to 7 into each row and column, whilst obeying the inequality signs (this means that the arrows should point at the lower number of each adjacent pair, where shown).
I’ve mixed up the already varied puzzle sizes a bit more in Sudoku Xtra issue 2, so several of the puzzle types that were all 9×9 in issue 1 are now at a range of sizes (mostly 6×6, 8×8, 9×9, 10×10). I’ve also tried to make sure the Skyscraper puzzles aren’t quite so tricky as last time round! In fact I’ve tried to make sure there’s a slightly wider range of difficulties on many of the types. This is something I’ll refine further over future issues, as I continue to find out what people think of the various puzzles.
I’m still putting the finishing touches to the issue, so I’d better get back to that now. Enjoy the Futoshiki!
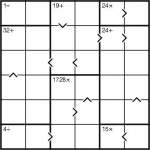
Inequality Calcudoku
Dec 10th
Here’s a fun little puzzle – a Calcudoku Inequality puzzle.
Just place 1 to 6 into each row and column whilst obeying the bold-lined cages’ operator totals. These give the result of applying the stated operator between all numbers in that region, so for example the result of adding together all the squares in a ‘24+’ region must be 24. Similarly the squares in the 1728x region must all multiply to that total. Unlike in Killer Sudoku, you can repeat a value within a cage (but you must still obey the constraint to not repeat a number in a row or column).
There are also some inequalities marked. These show that the value of one square is lower than the value of a square next to it. The arrow always points to the smaller number.
Good luck! ![]()
Samurai Star Inequality
Dec 8th
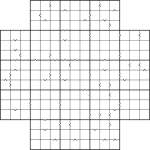
Samurai Star Inequality puzzle
I’m tempted to just say “good luck”, because frankly I think you’ll need it! Not of course in the literal sense, since this is an entirely logical problem, which requires absolutely no guess work, but in terms of finding the right areas to make progress quickly.
So having started at the end, let me introduce you to this Samurai Star Inequality puzzle. In all cases the “<” and “>” arrows point to the smaller number of each pair. Other than that it’s a regular Samurai Star – place 1 to 9 into each row, column and marked 3×3 box of each of the 5 underlying 9×9 grids (including the one in the centre).
And now back to the beginning: Good luck! ![]()
Inequality Sudoku
Dec 4th
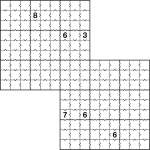
Inequality 2-grid Samurai Sudoku
Inequality jigsaw 6×6 Sudoku puzzle
On the Sudoku Xtra forums Marilyn suggested the great idea of an inequality Samurai puzzle for issue 2, so I’ve been having a look at doing this. And here’s the first result!
I’ve started off with a regular 6×6 jigsaw Sudoku, but have added inequalities, just to get you warmed up, then I’ve included my first ever Samurai Inequality Sudoku puzzle, albeit a 2-grid one for now.
You’ll notice in both puzzles here that I have included all inequality arrows, so you have far more information than you need – this is deliberate, to make them easier! On the 6×6 puzzle there are five really nice diamond shapes in the centre area, but in general I think having all the arrows is ugly (or lazy!) so I don’t plan to include them again in future (just as I’ve never included them in past published inequality/Futoshiki puzzles).
The rules of Inequality Sudoku are pretty simple – just place the numbers as you would in a regular Sudoku (or regular Jigsaw Sudoku in the 6×6 case), but obey the less-than (”<”) and greater-than (”>”) signs between squares. These indicate that the value of the number in a square is either less than or greater than its neighbour. And that’s it! ![]()
Good luck!

Recent Comments