Posts tagged Sudoku
Killer Sudoku Zero
Jun 20th
Zero Killer Sudoku 9×9 1 puzzleProbably because it sounded cool, or it was invented by someone who didn’t quite speak English, Killer Sudoku puzzles with some of the redundant clues removed are often referred to as ‘Zero’ Killer Sudoku. Or perhaps it’s because there are “zero redundant clues”. In any case, here’s one of those puzzles, where I have taken out all but the clues you definitely need to get a unique solution.
Usual Killer Sudoku rules apply: Place 1 to 9 in each row, column and bold-lined box as usual, but you must also ensure that each dashed-line cage adds up to the total given at the top-left of it. Numbers can not repeat in a dashed-line cage.
Speaking for myself, I found this puzzle really challenging to solve, but I can promise you that there’s no need to guess or use trial and error in any way – every deduction can be made using standard killer solving techniques.
Good luck! 
Diagonal Non-Consecutive Sudoku
Jun 19th
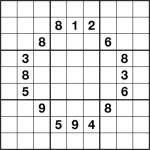
Sudoku Non-consecutive-diagonal 9×9 1 puzzleThis is a non-consecutive-diagonal sudoku puzzle. No digit may be diagonally-adjacent to a consecutive digit. But as you can see from the givens, consecutive numbers can be adjacent horizontally or vertically. What you can’t have, for example, is a 1 diagonally next to a 2 because the 1 & 2 are ‘consecutive’ (have a numeric difference of 1).
Consecutive Snake Sudoku
Jun 15th
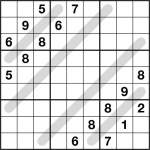
Sudoku Snake 9×9 1 puzzleHere’s something a little different – a consecutive snake sudoku.
Each of the shaded snakes consists of only ‘consecutive’ cells along its length, which means that any two cells joined by a snake must have values with a difference of 1, such as 2&3 or 7&8. So for example the 4-square-long snake at the top-left might have 2323 along its length, or any valid fit such as that.
In addition follow usual sudoku rules. Also note that only the cells joined by the snakes have any special relationship – any other pair of cells may or may not be consecutive (unlike in regular consecutive sudoku).
Trio Odd-Even Sudoku
Jun 14th
Sudoku Trio Odd/Even 9×9 1 puzzleI often post pretty challenging puzzles here, so I thought I’d entirely reverse that trend by publishing probably the easiest 9×9 puzzle with minimal givens you’ve ever seen.
Simply place 1-9 once each into every row, column and bold-lined region, as in a regular sudoku, but in this Odd/Even puzzle all of the even digits are in shaded cells. This is also a Trio sudoku too so each of the cells with an inset square contains 4, 5 or 6 and each of the cells with an inset circle contains 7, 8 or 9. Those without an inset square or circle contain 1, 2 or 3.
Using these rules you need only 3 givens for a valid unique puzzle. That’s the minimum number as you can probably easily convince yourself, because, despite its perhaps intimidating appearance, it’s essentially a set of trivial 1- and 2-digit sudokus laid on top of each other.
Jigsaw Blackout Sudoku
Jun 13th
Blackout Jigsaw Sudoku 9×9 puzzleIf you like tricky Sudoku variants, here’s one just for you! It’s a Blackout Sudoku with Jigsaw regions.
The rules are simple: in each row, column and bold-lined jigsaw region you must place 8 different digits in the range 1 to 9. Don’t place a digit on the shaded squares.
If you prefer you can consider it as a standard jigsaw sudoku where the black cell can represent any value, and the value can be different for the row, the column and the jigsaw region. For example the shaded square on the top row could take the place of a 7 in that row, an 8 in its column and a 2 in that jigsaw region.
Good luck!
King of Argyle Sudoku
Jun 8th
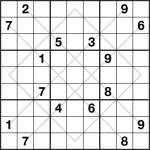
Sudoku Anti-King Argyle 9×9 1 puzzleSometimes it’s fun to mix variations together, so here’s a combination of Anti-king and Argyle Sudoku.
Anti-king means that no number repeats a “king’s move away in chess”. In practice this means that no two identical numbers touch in any direction, including diagonally.
Argyle means that no number repeats on any marked diagonal. The diagonals form an ‘Argyle’ Scots tartan pattern.
And since it’s a Sudoku, you must also place 1 to 9 in each row, column and bold-lined 3×3 box.
Good luck!
Frame Sudoku
Jun 7th
Frame Sudoku 9×9 1 puzzleHere’s a Frame Sudoku puzzle. Each number outside the grid gives the sum of the three nearest digits in that row or column, so for example if there is a 7 outside the grid then there must be a 1, 2 and 4 (1+2+4=7) in the first three cells in that row or column.
Regular Sudoku rules also apply – place 1 to 9 once each in all rows, columns and bold-lined boxes.
The actual logic in this is not especially tricky, but I certainly found it took me quite a while to test solve it (20 minutes or so, although I was watching TV…) – I’d be interested to know how long it takes you to solve it too!
Argyle Sudoku
Jun 1st
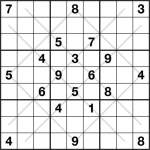
Sudoku Diagonal 9×9 1 puzzleI’m working on lots of different Sudoku variants for my forthcoming book, so I thought I’d post some of them here. On that basis, here’s an Argyle Sudoku puzzle. Just follow the usual rules but also note that you can’t repeat a digit in any of the marked diagonals.
You can now also keep track of this and future puzzles I publish using The Griddle’s puzzle tracking system. The following buttons update the status of the puzzle:
Non-Consecutive Sudoku
Mar 28th
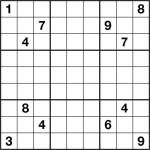
Non-consecutive Sudoku puzzleI’m currently working on a new book of sudoku variants for a major publisher, so have been making lots of new puzzles of different types. From time to time I’ll probably post again here with some examples of these.
I thought I’d start off with Non-Consecutive Sudoku. This is a minor variant on Consecutive Sudoku, where all the rules of standard Sudoku apply but there is one additional constraint:
- Neighbouring squares are not consecutive. This means there is never a difference of ‘1′ between two edge-adjacent squares (i.e. touching, not including diagonally).
For example, if a square contains ‘3′ then any neighbouring square cannot contain either ‘2′ or ‘4′.
Good luck!
Jigsaw Sudoku 6×6
Nov 18th
Jigsaw 6×6 puzzle 2
Jigsaw 6×6 puzzle 1I just made some Jigsaw Sudoku puzzles for a book and had a couple spare which I thought I’d post here. Just place A to F once each into every row, column and bold-lined jigsaw shape.
Recent Comments